Integration
Integration may be seen as the inverse process of differentiation. If we differentiate $y=4x^3+5$ we get $dy/dx=12x^2$ so if we integrate $12x^2$ we should get something like $4x^3+5$.
When we differentiate $4x^3$ we multiply the coefficient, $4$, by the exponent, $3$, then reduce the exponent by $1$. $\dfrac{d}{dx}(4x^3) = 3 \times 4x^2 = 12x^2$.
To integrate $12x^2$ we increase the exponent by $1$ then divide by the new exponent. $\int 12x^2 dx = 12x^3 / 3 = 4x^3$
But what happened to the $5$?
When we differentiate a constant like $5$ we get zero. When we integrate zero we don't know what we get so we call it $C$, the constant of integration. We won't know the value of $C$ until we know the boundary conditions.
Integrating Polynomial Expressions
If we differentiate the polynomial $y=ax^3+bx^2+cx+d$
we get $dy/dx=3ax^2+2bx+c$
We have differentiated the expression one term at a time.
$cx$ could be written as $cx^1$ when we reduce the exponent by $1$ we get $x^0$ which it equal to $1$ so $\dfrac{d}{dx}(cx)=c$.
$d$ could be written as $dx^0$. When we multiply by the exponent of $x$, which is $0$, the term becomes $0$ so $\dfrac{d}{dx}(d)=0$.
The process of differentiation was to multiply each coefficient by the exponent of the $x$ term and then reduced the exponent by $1$.
The process of integration is to increase the exponent of each $x$ term by $1$ then divide the coefficient by the new exponent.
Starting with $\dfrac{dy}{dx}=3ax^2+2bx+c$ we increase the exponent of each term by $1$ then divide the coefficient by the new exponent.
This gives us $y=ax^3+bx^2+cx$. Notice we have lost the $d$ term. We need to add the constant of integration $C$ until we know what value the constant term holds.
The result is $\int \dfrac{dy}{dx}dx = ax^3+bx^2+cx+C$ which is similar but not identical to the original expression.
Sanity Check
The best sanity check for integration is differentiation. When you have integrated an expression always differentiate it to see you get back to the starting point.
| Example 1 | ||
| Integrate $y=12x^3+6x^2+4x+5$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int 12x^3+6x^2+4x+5)dx$ |
| $=$ | $ \dfrac{12x^4}{4}+\dfrac{6x^3}{3}+\dfrac{4x^2}{2}+5x+C$ | |
| $=$ | $3x^4+2x^3+2x^2+5x+C$ | |
| Sanity Check | ||
| Differentiate $f(x)=3x^4+2x^3+2x^2+5x+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $4 \times 3x^3+3 \times 2x^2+2 \times 2x+5$ |
| $=$ | $12x^3+6x^2+4x+5$  | |
This is called an indefinite integral because we do not know the value of $C$. We keep $C$ until we can evaluate it by using the boundary conditions.
Table of Common Standard Integrals
The following table has a column of functions of $x$ ($y=f(x)$) on the left. The right hand column contains the integrals of the functions with respect to $x$ ($ \int f(x) dx=F(x)$).
| $y=f(x)$ | $ \int f(x) = F(x)$ |
|---|---|
| $x^n$ | $ \dfrac{x^{n+1}}{n+1}+C$ |
| $x^{-1}$ | $ ln(x)+C$ for $x>0$ |
| $ ln(-x)+C$ for $x<0$ | |
| $sin(ax)$ | $-cos(ax)/a+C$ |
| $cos(ax)$ | $sin(ax)/a+C$ |
| $tan(ax)$ | $ln(sec(ax))/a+C$ |
| $e^{ax}$ | $e^{ax}/a+C$ |
| $ln(ax)$ | $x(ln(ax)-1)+C$ |
| Example 2 | ||
| Integrate $y=cos(2x)$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int cos(2x)dx$ |
| $=$ | $\dfrac{sin(2x)}{2}+C$ | |
| Sanity Check | ||
| Differentiate $f(x)=\dfrac{sin(2x)}{2}+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $2 \times \dfrac{cos(2x)}{2}$ |
| $=$ | $cos(2x)$  | |
| Example 3 | ||
| Integrate $y=sin(3x)$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int sin(3x)dx$ |
| $=$ | $\dfrac{-cos(3x)}{3}+C$ | |
| Sanity Check | ||
| Differentiate $\dfrac{-cos(3x)}{3}+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $3 \times \dfrac{sin(3x)}{3}$ |
| $=$ | $sin(3x)$  | |
| Example 4 | ||
| Integrate $y=e^{3x}$ with respect to $x$ | ||
| $\int y\ dx$ | $=$ | $\int e^{3x}dx$ |
| $=$ | $e^{3x}/3+C$ | |
| Sanity Check | ||
| Differentiate $e^{3x}/3+C$ | ||
| $\dfrac{d}{dx}(f(x))$ | $=$ | $3 e^{3x}/3$ |
| $=$ | $e^{3x}$  | |
Integration by Substitution
Expressions that include a function of a linear factor may be integrated using a substitution.
If we want to integrate $(3x+4)^5$ we let $3x+4=u$.
Differentiating we get $du/dx=3$ so $dx=du/3$.
Substituting into the integral we get
| $I$ | $=$ | \( \int (3x+4)^5dx \) |
| $=$ | $\dfrac{1}{3}\int u^5du$ | |
| $=$ | $ \dfrac{1}{3} \dfrac{u^6}{6}+C $ | |
| $=$ | $ \dfrac{(3x+4)^6}{18}+C $ |
| Example 5 | ||
| $I=\int (4x-3)^3 dx$ | ||
| Let $u = 4x-3$ so $du/dx = 4$ or $dx = du/4$ | ||
| $I$ | $=$ | $\dfrac{1}{4}\int u^3 du$ |
| $=$ | $\dfrac{1}{4}(\dfrac{u^4}{4})+C$ | |
| Substituting $u = 4x-3$ | ||
| $I$ | $=$ | $\dfrac{(4x-3)^4}{16}+C$ |
| Sanity Check | ||
| $\dfrac{d}{dx}(\dfrac{(4x-3)^4}{16}+C)$ | $=$ | $\dfrac{4(4x-3)^3}{16} \times 4$ |
| $=$ | $(4x-3)^3$  | |
| Example 6 | ||
| $I=\int \dfrac{4}{2x-3} dx$ | ||
| Let $u = 2x-3$ so $\dfrac{du}{dx} = 2$ or $dx = \dfrac{1}{2}du$ | ||
| $I$ | $=$ | $4\int \dfrac{1}{2u} du$ |
| $=$ | $2\int \dfrac{1}{u} du$ | |
| $=$ | $2 ln(u)+C$ | |
| Substituting $u = 2x-3$ | ||
| $=$ | $2 ln(2x-3)+C$ | |
| Sanity Check | ||
| Differentiate $\dfrac{d}{dx}(2ln(2x-3)+C)$ | ||
| $\dfrac{d}{dx}(2ln(2x-3))$ | $=$ | $2 \times \dfrac{1}{2x-3} \times 2$ |
| $=$ | $\dfrac{4}{2x-3}$  | |
Definite Integration
Definite integration is where we integrate between two limits giving us the area between the curve and the axis.
Consider the equation $y=x^2+2$. If we integrate this between $x=1$ and $x=2$ we will get the shaded area shown in figure 1
$I = \int^2_1 x^2+2\ dx$
Integrating we get
$I = \dfrac{x^3}{3}+2x\ \Biggr|_{1}^{2}$
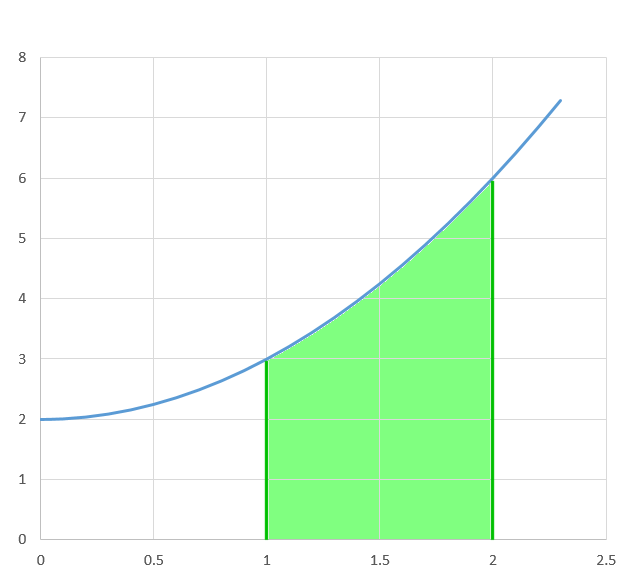
Notice there is no constant of integration. That is because we have the limits $x=1$ and $x=2$ which removes any uncertainty.
To evaluate the integral we find the value when we replace $x$ with $2$, the upper limit, and then subtract the value when we replace $x$ with $1$, the lower limit.
$I = \dfrac{x^3}{3}+2x\ \Biggr|_{1}^{2}$
$I = \dfrac{2^3}{3} + 2 \times 2 - (\dfrac{1^3}{3} + 2 \times 1)$
$I = \dfrac{8}{3}+4-(\dfrac{1}{3}+2) = \dfrac{20-7}{3} = \dfrac{13}{3}$
So the shaded area in figure 1 between $x^2+2$, $x=1$, $x=2$ and the $x$-axis is $13/3$.
| Example 9 | ||
| Integrate $\int^{\pi/2}_0 cos(\theta)\ d\theta$ | ||
| $I$ | $=$ | $\int^{\pi/2}_0 cos(\theta)\ d\theta$ |
| $=$ | $sin(\theta)\ \Biggr|_{0}^{\pi/2}$ | |
| $=$ | $1 - 0 = 1$ | |
What would happen if we integrated $cos(\theta)$ from $\pi/4$ to $3\pi/4$, the shaded area on figure 2?

| $I$ | $=$ | $sin(\theta)\ \Biggr|_{\pi/4}^{3\pi/4}$ |
| $=$ | $0.7071 - 0.7071 = 0$ |
which is clearly not right, the shaded area is not zero.
What we have to do in cases like this is notice the area is symmetrical about $\pi/2$ so we can calculate the area between $\pi/4$ and $\pi/2$ and then double it.
| $I$ | $=$ | $sin(\theta)\ \Biggr|_{\pi/4}^{\pi/2}$ |
| $=$ | $1 - 0.7071$ | |
| So the area $= 2 \times 0.2929 = 0.59$ | ||