Trigonometry
Sine and Cosine Rules
Figure 1 shows a triangle with sides a, b and c and angles subtending the sides A, B and C respectively.
Figure 1: Triangle with side lengths a, b and c.
For the triangle in Figure 1 we can write
$\dfrac{a}{sin(A)}=\dfrac{b}{sin(B)}=\dfrac{c}{sin(C)}$
These equations are called the sine rule.
Note: The sine of an angle, $\theta$, is the same as the sine of the supplement of the angle, $\pi - \theta$ ($180 - \theta$). This means the sine rule fails for triangles with an obtuse angle.
As a precaution, always calculate all three angles and add the results together. If the sum is less than $\pi$ ($180$) then the angle opposite the longest side is probably obtuse.
For the same triangle we can also write
$a^2=b^2+c^2-2bc\ cos(A)$
This equation is called the cosine rule.
When angle $A=\pi/2$, so we have a right angled triangle and the cosine rule simplifies to Pythagoras's theorem.
$a^2=b^2+c^2$
Figure 2: Right angle triangle.
For right angled triangles we can write
$sin(C)= \dfrac{c}{a}$, $cos(C)= \dfrac{b}{a}$ and $tan(C)= \dfrac{c}{b}$.
For angle $C$ side $b$ is called the adjacent, side $c$ is called the opposite and side $a$ is called the hypotenuse.
A common mnemonic for right angled triangles is SohCahToa which stands for:
$sin(C)=\dfrac{opposite}{hypotenuse}$, $cos(C)=\dfrac{adjacent}{hypotenuse}$, $tan(C)=\dfrac{opposite}{adjacent}$
A quick way to work out whether to use $sin()$ or $cos()$ to find a length is to imagine standing at angle $C$. Look along the adjacent side. We could say we were looking in the central direction and the central direction gives us $cos(C) = c/a$.
The opposite side goes sideways and sideways gives us $sin(\theta)=c/a$.
| Example 1 | |||
| Find the angles for a triangle with sides $a=4$, $b=5$ and $c=6$. | |||
| We need to use the cosine rule to find the first angle. | |||
| $a^2$ | $=$ | $b^2+c^2-2bc\ cos(A)$ | |
| $2bc\ cos(A)$ | $=$ | $b^2+c^2-a^2$ | |
| $$cos(A)$$ | $=$ | $\dfrac{b^2+c^2-a^2}{2bc}$ | |
| $$A$$ | $=$ | $cos^{-1}(\dfrac{b^2+c^2-a^2}{2bc})$ | |
| $$A$$ | $=$ | $cos^{-1}(\dfrac{5^2+6^2-4^2}{2 \times 5 \times 4})$ | |
| $$A$$ | $=$ | $0.72$ radians (or $41.41^\circ$) | |
| Similarly we get $B$ | |||
| $$B$$ | $=$ | $cos^{-1}(\dfrac{a^2+c^2-b^2}{2ac})$ | |
| $$B$$ | $=$ | $0.97$ radians (or $55.77^\circ$) | |
| and we get $C$ | |||
| $$C$$ | $=$ | $cos^{-1}(\dfrac{a^2+b^2-c^2}{2ab})$ | |
| $$C$$ | $=$ | $1.45$ radians (or $82.82^\circ$) | |
| Sanity Check | |||
| You might have been tempted to calculate two of the angles and subtract their sum from $\pi$ or $180^\circ$. If you did that you would have no easy way to check whether or not you had calculated three wrong angles. Better to calculate all three angles and add them together. | |||
| $0.72+0.97+1.45=3.14$ (or $41.41+55.77+82.82=180$) so we can be confident our answers are correct. | |||
Cartesian and Polar Coordinates
So far we have been sketching our diagrams on x-y axes. This system is attributed to René Descartes and is called the Cartesian coordinate system. The system allows us to describe any point on a 2D plane.
An alternative way to describe a point on a 2D plane is by giving an angle from a fixed line and a radius. This system is calle the polar coordinate system and is used a lot in navigation.
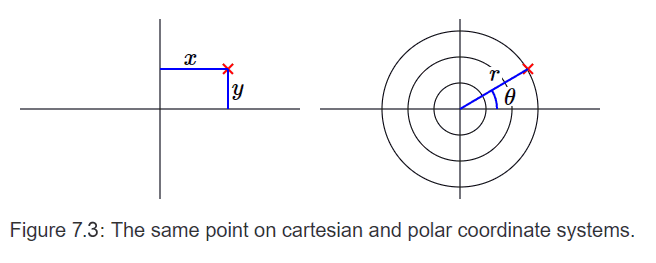
To convert from cartesian coordinates to polar coordinates we have:
$r^2=x^2+y^2$
$\theta = tan^{-1}(y/x)$
To convert from polar coordinates to cartesian coordinates we have:
$x=r\ cos(\theta)$
$y=r\ sin(\theta)$
3 Trigonometric Identities
Imagine a disc with a pen mounted near the edge. If the disc rotates about its centre the pen will draw a circle. Now, imagine there is a long strip of paper under the disc. If we pull the paper at a constant speed as the disc rotates, instead of a circle the pen will draw a wiggley line. The line is a sinusoidal curve and this is why sines, cosines and tangents are called circular functions.
Pythagoras's theorem states $x^2+y^2=r^2$. If we divide both sides by $r^2$ we get
$$(\dfrac{x}{r})^2+(\dfrac{y}{r})^2=1$$
Looking at figure 3 we can see $sin(\theta)= \dfrac{y}{r}$ and $cos(\theta)= \dfrac{x}{r}$ substituting these into our equation we get:
$$cos^2(\theta)+sin^2(\theta)=1$$
The angle $\theta$ was not used in our derivation which means $cos^2(\theta)+sin^2(\theta)=1$ is true for any value of $\theta$. This means the expression is more than an equation, it is an identity.
Here are some other trigonometric identities
$ \cos(\theta + \phi) = \cos(\theta)\cos(\phi)- \sin(\theta)\sin(\phi)$
$ \cos(\theta - \phi) = \cos(\theta)\cos(\phi)+ \sin(\theta)\sin(\phi)$
$ \sin(\theta + \phi) = \sin(\theta)\cos(\phi)+ \cos(\theta)\sin(\phi)$
$ \sin(\theta - \phi) = \sin(\theta)\cos(\phi)- \cos(\theta)\sin(\phi)$
$ \tan(\theta + \phi) = \dfrac{\tan(\theta)+ \tan(\phi)}{1-\tan(\theta) \tan(\phi)} $
$ \tan(\theta - \phi) = \dfrac{\tan(\theta)- \tan(\phi)}{1+\tan(\theta) \tan(\phi)} $
If we let $\theta = \phi$ we get
$ \cos(2\theta) = \cos^2(\theta)- \sin^2(\theta)$
$ \sin(2\theta) = 2 \sin(\theta)\cos(\theta)$
$ \tan(2\theta) = \dfrac{2\tan \theta}{1-\tan^2 \theta} $