Units
When Noah built his ark he measured the lengths in cubits and probably inches. A cubit is the length from your elbow to the tip of your big finger and an inch used to be the length of the top joint of your thumb before it was standardised. Units like these are convenient because you never have to carry a ruler.
Unfortunately, units like these are also inconvenient because one person's cubit may not be the same as anothers.
The International System of Units, called the SI system, is the world's official system of measurement. It has seven base units: second (s), metre (m), kilogram (kg), ampere (A), kelvin (K), mole (mol) and candela (cd). All other units are derived from the seven base units.
As an example of a derived unit, let's take the Newton. One Newton is defined as the force required to give a mass of 1kg an acceleration on $1ms^{-2}$. Putting this into equation form we would write:
$F = ma$
This is an equation so the left hand side equals the right hand side. That is true of the values. This is also true of the units.
The units on the left hand side are Newtons. The units on the right hand side are mass, measured in kilograms, multiplied by acceleration, measured in metres per second per second. So we can write:
Newtons = kilogram metres per second$^2$ or $N = kgms^{-2}$
Dimensional Analysis
We can generalise the analysis of units. Instead of using metres, kilograms and seconds we can use L for distance, M for mass and T for time.
Velocity is measured in units of length per unit of time. We can write this as LT$^{-1}$
Acceleration is measured in units of length per unit of time, per unit of time. We can write this as LT$^{-2}$
We know a force gives a mass an acceleration. That means the units of force are MLT$^{-2}$
Consistent Units
The units you use depends on what work you are doing. Golf ball manufacturers measure their output in hundreds of dozens, astronomers measure distances in astronomical units (1AU = 1.5x10$^{11}$m). When you are carrying out calculations you need to use a consistent set of units.
The two most common consistent sets of SI units are the metre-kilogram-second (MKS) and the centimetre-gram-second (CGS)
Conversion of Units
Life would be so much simpler if the World used a single consistent set of units. Sadly, that is not the case so we have to be adept at converting for one set of units to another.
As an example, imagine we wanted to convert metres per second (m/s) into miles per hour (mph). We know there are 1,760 yards in a mile , that there are 36 inches in a yard and exactly 25.4 millimetres in an inch. So, 1 mile = 1760 x 36 x 25.4 mm
| One hour has 60 minutes and 1 minute has 60 seconds so | ||
| 1 mph | = | (1760 x 36 x 25.4)/(60 x 60) mm/s |
| = | 1609344/3600 mm/s | |
| = | 447.04 mm/s | |
| = | 0.447 m/s | |
So 1mph is approximately 0.5m/s or 1m/s is approximately 2mph.
Below is a table of some common conversions.
| 1 | inch | = | 25.4 | millimetre |
| 1 | mile | = | 1.6093 | kilometre |
| 1 | pint (UK) | = | 0.5683 | litre |
| 1 | pound | = | 0.4536 | kilogram |
| 1 | ton | = | 1.0161 | tonne |
| 1 | millimetre | = | 0.0394 | inch |
| 1 | kilometre | = | 0.6214 | mile |
| 1 | litre | = | 1.7598 | pint (UK) |
| 1 | kilogram | = | 2.2046 | pound |
| 1 | tonne | = | 0.9842 | ton |
Prefixes
There is a system of 20 prefixes for large or small quantities, for example, a kilogram is 1000 grams. The prefixes are shown in the table below.
| Factor | Name | Symbol | Factor | Name | Symbol |
|---|---|---|---|---|---|
| $10^1$ | deka | da | $10^{-1}$ | deci | d |
| $10^2$ | hecto | h | $10^{-2}$ | centi | c |
| $10^3$ | kilo | k | $10^{-3}$ | milli | m |
| $10^6$ | mega | M | $10^{-6}$ | micro | µ |
| $10^9$ | giga | G | $10^{-9}$ | nano | n |
| $10^{12}$ | tera | T | $10^{-12}$ | pico | p |
| $10^{15}$ | peta | P | $10^{-15}$ | femto | f |
| $10^{18}$ | exa | E | $10^{-18}$ | atto | a |
| $10^{21}$ | zetta | Z | $10^{-21}$ | zepto | z |
| $10^{24}$ | yotta | Y | $10^{-24}$ | yocto | y |
Scientific Notation
Scientific notation, sometimes called standard form, has a single digit, 1 to 9, followed by an optional decimal part followed by 10 raised to a power. Take the number 987.65 as an example. In scientific notation we would write this as $9.8765 \times 10^2$
If we add $1$ to $9.8765 \times 10^2$ it becomes $1.9877 \times 10^2$ not $10.8765 \times 10^2$
If we wanted to write $9.8765 \times 10^2$ to two decimal places we would get $9.88 \times 10^2$
Engineering Notation
Engineering notation has a zero or more digits followed by an optional decimal part followed by 10 raised to a power that is a multiple of 3. The power is based on the prefixes listed above.
Imagine you have a file that is 654321 bytes long. If someone asked you how big the file was you probably wouldn't say 654321 bytes. You might say 654 kilobytes. You might say 0.65 megabytes. In engineering notation thess would be $654.321 \times 10^3$b or $0.65 \times 10^6$b respectively. $10^3$ is kilo and $10^6$ is mega.
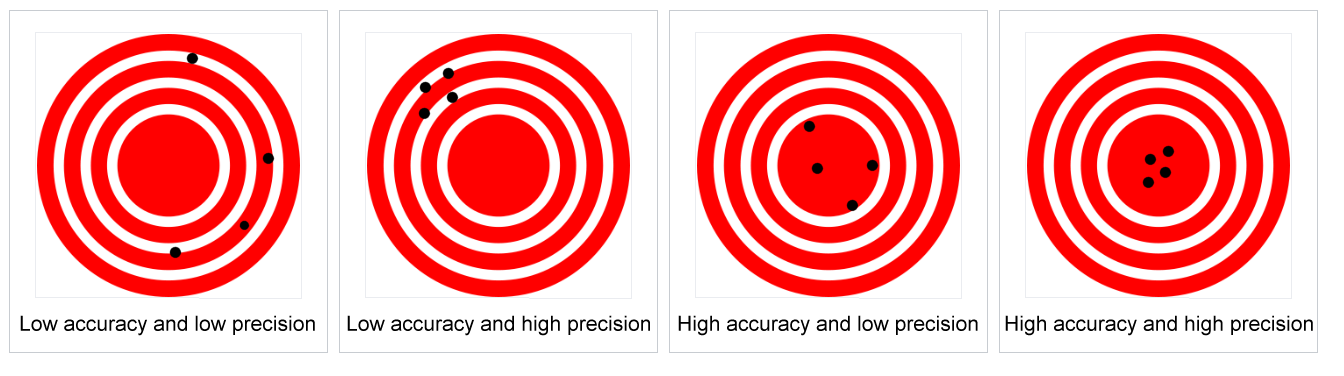
Accuracy and Precision
Accuracy is how close a measurement is to the true value. Precision is how close measurements are to each other.
Significant Figures
Significant figures are the figures in a number that carry meaning There are four rules on how to determine how many significant figures there are in a number.
Rules on significant figures
- Non-zero digits are always significant.
- Any zeros between two significant digits are significant.
- Leading zeros are never significant.
- Trailing zeros are only significant in the decimal part of a number.
Let's look at some examples.
| Rule 1 | $12.34$ has four non-zero digits so it has four significant figures. |
| Rule 2 | $102.304$ has four non-zero digits and two zeros each between significant figures. That makes both the zeros significant so there are six significant figures. |
| Rule 3 | $0.003$ has a leading zero before the decimal point and two leading zeros after. They are not significant. There is one non-zero digit so the number has one significant figure. |
| Rule 4 | $600$ has one non-zero digit and two trailing zeros so it has one significant figure. |
| Rule 4 | $6.2600$ has three non-zero digits and two trailing zeros after the decimal point so it has five significant figures. |
Modelling Data
Sanity Check
A wise person never does a calculation without a sanity check. A sanity check is an estimate of the answer, preferrably by a different route. If your answer and sanity check are different you know at least one of them is wrong. If they are similar then they might be correct. Next, ask yourself does the answer seem reasonable?
For example, imagine you did a calculation about an oil tanker and determined the tanker was travelling at 50 ms$^{-1}$.
Next you did a sanity check and found a different answer. You review your assumptions, redo your calculations and get the two values to be close enough to 50 ms$^{-1}$.
So far so good.
Finally, you remember that 1 ms$^{-1}$ is approximately 2 miles per hour which means your tanker is travelling at about 100 mph. Now you know something is wrong with the calculation.